Research
研究
プラズマ乱流におけるマルチスケール性
Multi-scale nature of plasma turbulence
磁場閉じ込めプラズマ中では、その内部エネルギーを駆動源として様々な波動が励起されます。質量が1800倍程度異なる電子とイオンでは、それぞれの運動に特徴的な波が不安定化し、異なるスケールの乱流を作り出します。従来はスケール分離を仮定して独立に研究が行われてきましたが、最近の研究で両者が相互作用することが分かってきました。


プラズマ乱流における磁場揺動効果
Effects of electromagnetic fluctuations on plasma turbulence
プラズマ乱流はこれまで静電近似の下で、磁場の揺らぎを無視した解析が主に行われてきました。しかし、核融合プラズマの高性能化に伴い、微視的な乱流においても磁場揺動の効果が重要となることが示唆されています。磁場揺動はアルヴェン波の伝搬や磁場構造の微視的ティアリングなど、静電揺動とは異なる乱流現象を引き起こします。
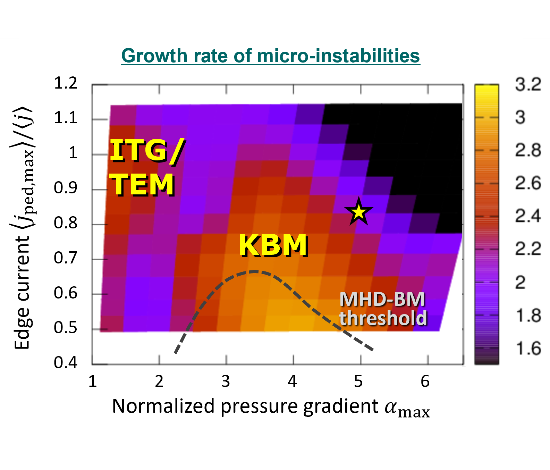

プラズマ乱流における運動論効果
Kinetic effects in plasma turbulence
プラズマ乱流は、対流を引き起こすだけでなく、位相空間における混合過程を引き起こします。磁力線平行方向の弾道的な運動による混合や磁力線垂直方向のサイクロトロン運動に起因する混合といった素過程は、核融合プラズマの乱流のみならず太陽風乱流などにも通じる一般的な現象と考えられています。
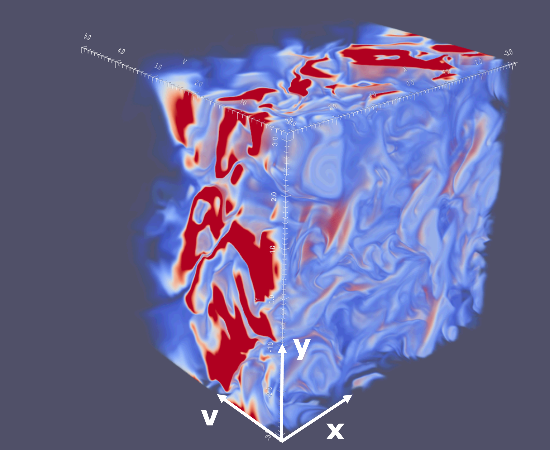

プラズマ乱流の高性能計算
High performance computing of plasma turbulence
マルチスケール性・電磁揺動・運動論などの様々な効果を取り入れたプラズマ乱流の数値シミュレーションを行うには、スーパーコンピュータの利用が不可欠です。最新のスーパーコンピュータは、複数の計算ノードをネットワークで接続した大規模並列計算機であり、日進月歩で研究開発が進められているため、その性能を引き出すにはシミュレーションコードの並列計算技術も併せて進めていく必要があります。
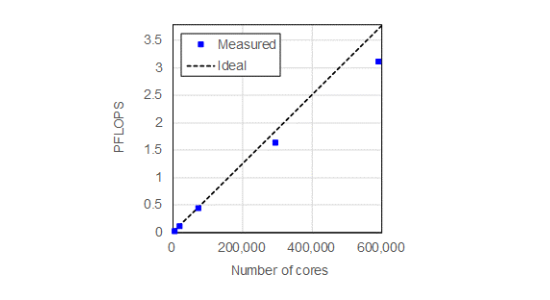

乱流の非線形相互作用解析
Analyses of nonlinear interactions in turbulence
プラズマ乱流の複雑な非線形相互作用をシミュレーションデータから抽出するために、流体力学の伝統的な解析手法である三波相互作用解析、非平衡統計物理に端を発する森-Zwanzigの射影演算子法、データ科学的手法の一つであるマルチフィデリティモデリングなど、多様な方法論をプラズマ物理の観点から拡張・応用しています。
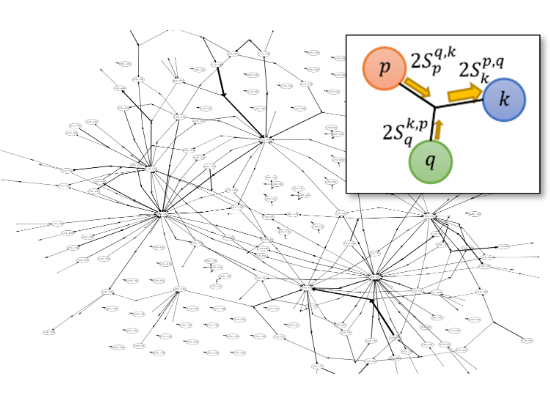

Projects
研究プロジェクト
JST戦略的創造研究推進事業 さきがけ [複雑流動]
研究課題:”磁化プラズマ乱流のマルチスケール・マルチフィデリティモデリング”
Multi-scale and multi-fidelity modeling of magnetized plasma turbulence

2020.4 - 2023.3
スーパーコンピュータ「富岳」成果創出加速プログラム
研究課題:”核燃焼プラズマ閉じ込め物理の開拓”
Exploration of burning plasma confinement physics using the Supercomputer Fugaku

Outputs
研究成果
ソフトウェア
Softwares
ジャイロ運動論的Vlaosvシミュレーションコード: GKV (共同開発)
GyroKinetic Vlasov simulation code: GKV (jointly developed)
https://github.com/GKV-developers
https://www.p.phys.nagoya-u.ac.jp/gkv/

森-Zwanzigの射影演算子法Pythonモジュール: mzprojection
Python module for Mori-Zwanzig projection operator method: mzprojection
https://github.com/smaeyama/mzprojection
概要:
射影演算子法に基づく統計的時系列データ解析により、目的変数の説明変数に対する相関・無相関部分を抽出する。
(1) ユーザは、解析したい目的変数f(t)と説明変数g(t)の時系列データアンサンブルを所定の配列形式で用意する。
(2) Pythonモジュールをインポートした後、関数にデータを渡すことで f(t) の g(t) に対する射影
f(t) = omega*g(t) + s(t) + r(t)
s(t) = - \int_0^t memoryf(t)*g(t-v) dv
が計算され、Markov係数 omega や記憶関数 memoryf(t)、無相関項 r(t) などの情報が得られる。
※時系列データの長さが記憶時間に比べて短かすぎたり、アンサンブルの標本数が少なすぎたりすると、正しい結果が得られない場合(典型的には、記憶関数が十分減衰しない、無相関項r(t)と興味変数の初期値g(0)との相関が有意に残る、など)があるので、収束性を確認すること。
理論の詳細については、日本語論文もあるのでこちらも併せてご覧ください。
三つ組み相互作用の有向表現Pythonモジュール: triadgraph
Python module for directional representation of triad interactions: triadgraph
https://github.com/smaeyama/triadgraph
概要:
乱流相互作用を表す二次の非線形項に由来する三つ組みエネルギー伝達を有向表現・ネットワーク可視化により解析する。
(1) ユーザーは対称化伝達関数(または非対称化伝達関数)のデータセットを所定の配列形式で用意する。
(2) Pythonモジュールをインポートした後、関数にデータを渡すことで、対称化伝達関数と整合しつつ三つ組み間の循環の任意性を除外した1対1伝達関数として有向表現が得られる。
(3) さらに、ネットワーク可視化パッケージである PyGraphviz を利用することで、対称化伝達関数または有向表現のネットワーク可視化が行える。
理論の詳細については、原著論文をご覧ください。三つ組み相互作用や有向表現などの手法の議論は、プラズマ乱流に関する専門知識不要で読み進められる内容です。
マルチフィデリティモデリングPythonモジュール: mfmodeling
Python module for multi-fidelity modeling: mfmodeling
https://github.com/smaeyama/mfmodeling
概要:
理論・シミュレーション・実験などから得られるデータには、現象を記述する忠実度(フィデリティ)やデータ点数、パラメータ範囲の異なる多様なデータが存在する。マルチフィデリティモデリングは、高精度だが少数の高フィデリティデータの不足を、低精度だが多数の低フィデリティデータとの相関を利用することで補い、全体としての予測精度を高める方法論である。
非線形自己回帰ガウス過程回帰(Nonlinear Auto-Regressive Gaussian Process regression; NARGP)と呼ばれる手法[Perdikaris (2017)]を用いたマルチフィデリティ回帰を行う。
(1) ユーザーは回帰したい入出力のデータセットを用意する。この際、階層的なマルチフィデリティ問題設定を想定し、各フィデリティ毎に入出力のセットが存在する。
data_list = [[data_low_fid_x, data_low_fid_y],
[data_med_fid_x, data_med_fid_y]],
[data_high_fid_x, data_high_fid_y]]
(2) Pythonモジュールをインポートした後、NARGPクラスにデータを渡すことで、NARGPによるマルチフィデリティガウス過程回帰モデルが作成される。
(3) 作成されたモデルを用いて任意の入力に対する期待値および予測分散が得られる。
理論の詳細については、原著論文をご覧ください。
主著論文の一言解説
Brief explanations on first-author articles
"Multi-fidelity information fusion for turbulent transport modeling in magnetic fusion plasma", S. Maeyama, M. Honda, E. Narita, S. Toda, Scientific Reports 14, 28242 (2024).
https://doi.org/10.1038/s41598-024-78394-3
マルチフィデリティモデリングは、予測に使いたい高精度なデータ(高フィデリティデータ)が少ない場合でも、その不足を補うために、精度は低くても数が多いデータ(低フィデリティデータ)を利用して予測精度を高める方法論である。本研究では、非線形自己回帰ガウス過程回帰(Nonlinear Auto-Regressive Gaussian Process regression, NARGP)というマルチフィデリティデータ融合手法を導入し、(i)低・高解像度シミュレーションデータの統合、(ii)核融合プラズマ実験データに基づく乱流拡散係数の予測、(iii)簡易理論モデルと乱流シミュレーションデータの統合などの事例に適用し、マルチフィデリティデータ融合手法によってプラズマ乱流輸送モデルの予測精度が向上することを実証した。
以前から、大規模シミュレーションで物理の理解が進展したという学会発表の際に、「(計算の軽量な)輸送モデルに反映できますか?」というような質問を受けて、「大規模シミュレーションを直接すぐに装置設計に使われているような低コストの簡易モデルに落とし込めるわけではない」という回答をするのは内心忸怩たる思いがあった。おぼろげに「大規模シミュレーションによる高精度データがあるならば、データ数は少ないとはいえそれを上手く活用することで、既存の低精度簡易モデルをより高精度化することができるはず」と思っていたものを、マルチフィデリティ回帰として具体化できた。輸送モデルに限らず汎用的な手法なので、興味を持っていただいた方は、適用可能なデータセットがあれば、GitHubからダウンロードしてすぐに試してもらえる。「もしかしてあなたの取り組んでいる問題もマルチフィデリティかも?」
"Rotating flux-tube model for local gyrokinetic simulations with background flow and magnetic shears", S. Maeyama, T.-H. Watanabe, M. Nakata, M. Nunami, Y. Asahi, A. Ishizawa, Journal of Computational Physics 522, 113595 (2025).
https://doi.org/10.1016/j.jcp.2024.113595
平衡径電場による背景シア流がある場合の局所ジャイロ運動論シミュレーションのために、回転フラックスチューブと名付けた新しい数値解法を考案した。「シア流に沿って座標変換したフラックスチューブかな」と思った人は3割くらい正解だがほぼ不正解。タイトルにもある通り磁気シアがあることが重要で、正確には「シア流に沿った磁力線垂直方向の座標変換による形状のねじれを、磁気シアによる磁力線方向への形状のねじれで打ち消すように、磁力線方向への並進移動も同時に行うフラックスチューブ」モデルである。文章だけではイメージしにくいと思うが、論文オンラインページにはわかりやすい動画もSupplementary materialとして用意した。論文中でも述べたが、アナロジーとしては、ねじとねじ穴の関係を考えてもらうと良い。固定されたねじ穴に対してねじを(差動)回転させる速度がシア流のせん断率に対応し、ねじのピッチ(の逆数)が磁気シアに対応する。ねじ(シミュレーションボックス)の形状を変形させずに一定の回転速度(シア流のせん断率)でねじを回そうとすると、そのピッチ(磁気シアの逆数)に応じてねじは前進または後退(磁力線方向への並進移動)する。
上述の技巧的な面白さだけでなく、周期性を持つ時間依存演算子で記述されるFloquetの一般化固有値問題との数学的対応が明らかになる、線形モードを単一波数のモードとして表現できるため従来はできなかったシア流存在下での三波相互作用解析が可能になるなどの新規の利点がある。さらに、シア流存在下の亜臨界不安定性やそれに伴うヒステリシス、非軸対称系での磁力線ラベル依存性を取り入れる拡張など、物理的に興味深い今後の展開がいくつかある。
"Overview of multiscale turbulence studies covering ion-to-electron scales in magnetically confined fusion plasma", S. Maeyama, N. T. Howard, J. Citrin, T.-H. Watanabe, T. Tokuzawa, Nuclear Fusion 64, 112007 (2024).
https://doi.org/10.1088/1741-4326/ad34e1
電子・イオン系マルチスケールプラズマ乱流について、2014年頃から続けてきた自身の理論・シミュレーションの仕事を含め、実験的な重要性や、モデリングの進展状況について、IAEA核融合エネルギー会議でのオーバービュー講演で発表した内容をまとめたレビュー論文。レビューと呼ぶには短いが、その分重要な着眼点だけを簡潔にまとめた。
実は、世界的にも電子スケール乱流効果についての進展をまとめておこうという機運があったようで、全く独立に同時期に以下のレビュー論文も出版されている。
"Transport from electron-scale turbulence in toroidal magnetic confinement devices", Y. Ren, W. Guttenfelder, S. M. Kaye, W. X. Wang, Review of Modern Plasma Physics, 8:5 (2024) (第一著者のYang RenはNSTX装置などで電子スケール揺動計測もされた実験・計測の専門家)
https://doi.org/10.1007/s41614-023-00138-z
現時点では未出版のようなので明記できないが、米国の輸送モデリングの研究者の方からもレビュー論文を書いていると小耳にはさんだので、
理論[Maeyama (2024)]-モデリング[出版されたら追記]-実験・計測[Ren (2024)]と、それぞれの専門の観点から見たレビューを見比べて差異を楽しめるだろう。
本論文に関しては、特にマルチスケールプラズマ乱流相互作用の物理性質の理解に向けた第3節で、これまでの理論・シミュレーション研究を横断的に俯瞰して、スケールの離れた乱流間の相互阻害性(お互いに邪魔しあうこと)という普遍的な性質を独自の視点を提案している。第6節でもまとめたように、不安定駆動される乱流揺動だけでなく帯状流などの非線形構造も混在したプラズマ乱流中では、乱流間の相互阻害性は必ずしも輸送低減を意味しない点には注意。
"射影演算子による統計的時系列データ解析とその応用", 前山伸也, 三分一史和, 統計数理 71, 25-45 (2023).
"Statistical Analysis of Time-series Data Using the Projection Operator Method and Its Application", Shinya Maeyama, Fumikazu Miwakeichi, Proceedings of the Institute of Statistical Mathematics Vol. 71, No. 1, 25–45 (2023). (In Japanese)
https://www.ism.ac.jp/editsec/toukei/pdf/71-1-025.pdf
https://github.com/smaeyama/maeyama_toukeisuri_2023
時系列データ解析としてみると、影演算子法は興味ある目的変数の時間発展を、説明変数に対する相関項と無相関項に分離し、一般化 Langevin 形式で記述する。本研究では、その定式化を再訪しつつ、連続時間および離散時間システムでの任意の目的・説明変数に対する拡張を行った。続いて、類似した時系列データ解析手法として構造ベクトル自己回帰(SVAR)モデルとの比較を行った。射影演算子法は任意の説明変数に対する定式化でありSVAR モデルよりも広い適用範囲を持つこと、説明変数として自己回帰形を用いた場合はSVAR モデルと同等の相関を抽出可能であることを示した。さらに応用例として、プラズマ乱流による帯状流生成・維持過程を一般化 Langevin 方程式として捉える解釈を提案し、射影演算子法による時系列データ解析に基づく根拠を与えた。以上により、物理的解釈を与えるためのデータ解析、および、確率的時系列データのモデリングに対する射影演算子法の有用性を示した。開発した手法は Python からのシンプルな関数呼び出しで利用できるオープンソースコードとして公開し、興味を持った読者は手軽に試すことができる。(和文誌ですが、研究ノートや詳解記事ではなく、原著論文です)
"Multi-scale turbulence simulation suggesting improvement of electron heated plasma confinement", Shinya Maeyama, Tomo-Hiko Watanabe, Motoki Nakata, Masanori Nunami, Yuuichi Asahi, and Akihiro Ishizawa, Nature Communications 13, 3166 (2022).
https://doi.org/10.1038/s41467-022-30852-0
https://github.com/smaeyama/maeyama_ncomm_2022
これまで電子・イオンスケール乱流間のマルチスケール相互作用について調べてきたが、果たしてこうしたマルチスケール相互作用は将来の核燃焼プラズマでも有意に働きうるのだろうか。核燃焼時の電子加熱かつ多粒子種混合プラズマという特徴を模擬して、高電子温度かつ電子、燃料種重水素・三重水素、ヘリウム燃焼灰からなる多成分プラズマに対し、スーパーコンピュータ「富岳」による大規模並列計算を駆使したマルチスケール乱流シミュレーションを行った。その結果、核燃焼で想定されるような高電子温度領域でもマルチスケール相互作用が存在しうること、それにより電子のみならず、燃料イオン種やヘリウム灰の輸送についても影響を受けることを明らかにした。また、マルチスケール相互作用を介した輸送低減が起こりうることを新たに示した。
"Effects of ion polarization and finite-β on heat transport in slab electron-temperature-gradient driven turbulence", Shinya Maeyama, Seiya Kusaka, and Tomo-Hiko Watanabe, Physics of Plasmas 28, 052512 (2021).
https://doi.org/10.1063/5.0044435
長波長のスラブETG不安定性はイオン分極効果による電場の増強による成長率増大や、電子表皮長程度の磁場揺動に伴う反磁性効果を介した電子圧力揺動の減少による成長率減少などの影響を受ける。これら長波長モードの線形成長率の変化は、非線形乱流状態では揺動振幅に大きな影響を与えうる。線形解析については流体描像との対応を含め本論文で非常にすっきりまとまった。一方で、非線形乱流でどのような構造ができるかは、帯状流に対するRhinesスケール、渦の結晶化構造のスケール[C. Kawai, et al., Phys. Plasmas 24, 042303 (2017)]、イオンジャイロ半径、電子表皮長などの複数のスケールが関与するが、これらは異なるパラメータ(密度勾配、電子・イオン温度比、イオン質量、プラズマベータ値)にほぼ独立に依存するため、今後の課題としてこれらのパラメータを系統的にスキャンすることで、どういった機構で構造が分岐するか、形成される構造を自由自在にコントロールできるかといった研究が展開できると思うが、時間が取れないので興味を持つ学生・共同研究者がいたら取り組んでみたい。
"On the triad transfer analysis of plasma turbulence: symmetrization, coarse graining, and directional representation”, Shinya Maeyama, Makoto Sasaki, Keisuke Fujii, Tatsuya Kobayashi, Richard O. Dendy, Yuichi Kawachi, Hiroyuki Arakawa, Shigeru Inagaki, New Journal of Physics 23, 043049 (2021).
https://doi.org/10.1088/1367-2630/abeffc
https://github.com/smaeyama/triadgraph
様々な乱流は二次の非線形性に起因し、そのエネルギー伝達は異なるモード間の三つ組み相互結合として記述される。乱流の研究では古くから三つ組み相互作用の対称性について注意が払われ、対称化エネルギー伝達関数が解析されてきた。一方で、非対称エネルギー伝達関数の反対称性を拠り所として1対1相互作用によりモード間結合を表す提案もあり、特に電磁流体力学的乱流や微視的プラズマ乱流の研究で広く用いられてきた経緯がある。この論文では、非対称エネルギー伝達関数の不定性の問題と対称化の重要性を再訪しつつ、対称化エネルギー伝達関数と整合した1対1相互作用として記述する三つ組み相互作用の有向表現を提案している。
本論文で新提案した有向表現の是非は一旦置いておいたとしても、見かけのエネルギー伝達を含みうる非対称エネルギー伝達関数を不用意に使っている論文も多く見られる宇宙・核融合・プラズマ研究者の方には、せめて非対称エネルギー伝達解析の不定性および対称化の重要性だけでも一度読んで考えてほしい。
日本語の参考文献:前山伸也, "三波エネルギー伝達関数の対象化と有向表現", 日本流体力学会年会2021予稿.
"Extracting and Modeling the Effects of Small-Scale Fluctuations on Large-Scale Fluctuations by Mori-Zwanzig Projection Operator Method”, Shinya Maeyama, and Tomo-Hiko Watanabe, Journal of the Physical Society of Japan 89, 024401 (2020).
https://doi.org/10.7566/JPSJ.89.024401
https://github.com/smaeyama/mzprojection
射影演算子法は非平衡統計物理分野で開発された数理手法であり、興味変数の支配方程式を一般化Langevin方程式の形で記述する。単に形式論として引用されることもあるが、本論文では、実用的なデータ解析として用いるための方法論とその適用事例について解説した。具体的には、マルチスケール乱流相互作用を異なるスケールの乱流間の相関問題として捉え、射影演算子法を適用することで、興味変数(=大スケール流れ)の支配方程式に対する、その他の変数(=小スケール揺らぎ)の寄与を興味変数に相関を持つコヒーレント項をノイズ的な無相関項に分離する手法を新たに考案した。
"Implementation of a gyrokinetic collision operator with an implicit time integration scheme and its computational performance”, Shinya Maeyama, Tomo-Hiko Watanabe, Yasuhiro Idomura, Motoki Nakata, and Masanori Nunami, Computer Physics Communications 235, 9 (2019).
https://doi.org/10.1016/j.cpc.2018.07.015
クーロン衝突周波数は速度の3乗に逆比例するため、詳細な衝突項を用いて運動論シミュレーションを行う場合、電子-イオン衝突項により時間刻み幅が厳しく律速されうる。本論文では、作用素分割法と半陰解法およびクリロフ部分空間法を組み合わせた汎用解法を用いて、係数行列が密となるジャイロ運動論的線形衝突項の陰解法実装を行った。衝突項が速度空間のみに依存する差分オペレータであることに着目し、転置通信を利用することで、陰解法における反復計算をMPI通信フリーに実装する。これにより、演算性能の向上と求解時間の短縮の両方を実現した。
"Suppression of Ion-Scale Microtearing Modes by Electron-Scale Turbulence via Cross-Scale Nonlinear Interactions in Tokamak Plasmas”, Shinya Maeyama, Tomo-Hiko Watanabe, and Akihiro Ishizawa, Physical Review Letters 119, 195002 (2017).
https://doi.org/10.1103/PhysRevLett.119.195002
電子・イオンスケール乱流間の相互作用解析はこれまで電子・イオン温度勾配不安定性により駆動される乱流に限られていたが、新たにマイクロティアリングモードと電子温度勾配モードの間の相互作用を解析した。その結果、電子温度勾配モードの作り出す流れが、マイクロティアリングモードの電流シート構造を破壊することで、マイクロティアリングモードを安定化する働きが発見された。このことは、電子とイオンの中間的なスケールの構造(サブイオンスケール構造)を介したマルチスケール相互作用という描像の普遍性を支持する。
“Cross-scale interactions between electron and ion temperature gradient driven turbulence via sub-ion-scale structures”, Shinya Maeyama, Tomo-Hiko Watanabe, Yasuhiro Idomura, Motoki Nakata, Akihiro Ishizawa, and Masanori Nunami, Nuclear Fusion 57, 066036 (2017).
https://doi.org/10.1088/1741-4326/aa687c
電子・イオン温度勾配不安定性駆動マルチスケール乱流のスケール間相互作用を詳しく解析した。非線形性によるエントロピー伝達関数の流体近似や部分空間伝達解析手法を新たに考案し、それを利用することで、①イオンスケール乱流渦が電子スケール乱流をせん断する働きや②イオンスケール乱流が作り出す短波長帯状流を電子スケール乱流が減衰させる働きを明らかにした。これにより、電子とイオンの中間的なスケールの構造(サブイオンスケール構造)を介したスケール間相互作用という、マルチスケール乱流の新たな描像が見えてきた。
“Benchmark of Electromagnetic Gyrokinetic Codes in High Performance Fusion Plasma”, Shinya Maeyama, Tomo-Hiko Watanabe, Hauke Doerk, Motoki Nakata, and Akihiro Ishizawa, Plasma and Fusion Research 11, 2403011 (2016).
https://doi.org/10.1585/pfr.11.2403011
実際の実験データ・磁場配位に基づいた、マイクロティアリングモードを含む電磁的ジャイロ運動論シミュレーションについて、GKVコード・GENEコード間でベンチマークテストを行い、両者の良好な一致を確認した。また、マイクロティアリングモードの線形モード構造を調べ、磁場ドリフトによる通過電子の有限軌道幅により、電流がトーラス外側でO型構造となることを明らかにし、電流構造の広がり幅の理論的な見積もりを与えた。(博士課程時代に留学したマックスプランクプラズマ物理研究所の友人のHaukeとの共著。ASDEX-Upgradeの実験データを用意してもらったり、マイクロティアリングモードに関する知見をいろいろと教えてもらったり、とても助けられた。共同研究プロジェクトのきっかけをくれたHeliosにも感謝。)
“Cross-Scale Interactions between Electron and Ion Scale Turbulence in a Tokamak Plasma”, Shinya Maeyama, Yasuhiro Idomura, Tomo-Hiko Watanabe, Motoki Nakata, Masatoshi Yagi, Naoaki Miyato, Akihiro Ishizawa, and Masanori Nunami, Physical Review Letters 114, 255002 (2015).
https://doi.org/10.1103/PhysRevLett.114.255002
電子ラーマ半径スケールで起こる電子温度勾配不安定性駆動乱流と、イオンラーマ半径スケールで起こるイオン温度勾配不安定性駆動乱流が相互作用することを明らかにした。特に、①イオンスケール乱流により電子スケール乱流が抑制されること、②電子スケール乱流が帯状流を減衰させることにより、結果的にイオンスケールの乱流輸送を増大させ得ることを示した。これらの結果から、イオン温度勾配不安定性が十分に不安定な場合はイオンスケールのみ扱う従来的な単一スケール乱流解析が輸送レベルの良い見積もりを与えるが、イオンスケールの不安定性が弱い場合には電子スケールの影響が無視できず、マルチスケール解析が必要となるという警告を与えた。(ほぼ同時期に、実験で観測された熱輸送を説明するのにマルチスケール解析が必要であるというHowardらの報告もあるので併せて参照されたい。)
“Improved strong scaling of a spectral/finite difference gyrokinetic code for multi-scale plasma turbulence”, Shinya Maeyama, Tomo-Hiko Watanabe, Yasuhiro Idomura, Motoki Nakata, Masanori Nunami, and Akihiro Ishizawa, Parallel Computing 49, 1 (2015).
https://doi.org/10.1016/j.parco.2015.06.001
京コンピュータにおけるジャイロ運動論的シミュレーションコードGKVの並列計算手法開発成果についてまとめた論文。多次元領域分割、3次元トーラスネットワークにおける区分化プロセス配置、OpenMPを用いた通信と演算のパイプライン化オーバーラップなどの手法を提案し、並列計算の粒度とレイテンシ・ロードインバランス・スケジューリングオーバーヘッドなどについて議論し、100万コア級のストロングスケーリングを実証した。
“Multi-Scale ITG/TEM/ETG Turbulence Simulations with Real Mass Ratio and Beta Value”, Shinya Maeyama, Yasuhiro Idomura, Motoki Nakata, Masatoshi Yagi, and Naoaki Miyato, Proceedings in 25th IAEA Fusion Energy Conference, TH/1-1 (2014).
電磁的ジャイロ運動論に基づき、電子スケールからイオンスケールまで扱うマルチスケール乱流の直接数値シミュレーションを行い、水素・電子実質量比かつ実験で観測されたプラズマベータ値での解析において、従来のスケール分離の過程を覆す電子・イオンスケール間相互作用が起こること、それにより乱流輸送が大きく変化しうることを示した。(初参加のIAEA核融合エネルギー会議で口頭発表の大役を任され、緊張するやら興奮するやら愉しみやらで、とにかく集中して発表に臨んだ記憶がある。)
“Comparison between kinetic-ballooning-mode-driven turbulence and ion-temperature-gradient-driven turbulence”, Shinya Maeyama, Akihiro Ishizawa, Tomo-Hiko Watanabe, Motoki Nakata, Naoaki Miyato, Masatoshi Yagi, and Yasuhiro Idomura, Physics of Plasmas 21, 052301 (2014).
https://doi.org/10.1063/1.4873379
従来多くの解析がなされているイオン温度勾配不安定性駆動乱流との比較という観点から、運動論的バルーニングモード駆動乱流の性質を調べた。粒子・場相互作用を介した電子揺動生成、電子の通過的運動が作り出す微細構造、帯状流を介すことなく飽和に至る非線形相互作用機構などの特徴が明らかとなった。(ただし、電子温度勾配による駆動がない場合の解析結果である。より一般的なパラメータスキャンや、大域的分布効果なども考慮されるべき課題として挙げられた。)
“Kinetic Ballooning Mode Turbulence Simulation based on Electromagnetic Gyrokinetics”, Shinya Maeyama, Akihiro Ishizawa, Tomo-Hiko Watanabe, Motoki Nakata, Naoaki Miyato, and Yasuhiro Idomura, Plasma and Fusion Research 9, 1203020 (2014).
https://doi.org/10.1585/pfr.9.1203020
運動論的バルーニングモードの非線形シミュレーションを行い、その飽和機構を議論した。特に、電子温度勾配による駆動がない場合には、E・J項による電磁揺動を介したイオンから電子へのエントロピー伝達が起こり、イオンと電子の散逸効果の両方が効いて飽和に至ることが示された。
“Computation-Communication Overlap Techniques for Parallel Spectral Calculations in Gyrokinetic Vlasov Simulations”, Shinya Maeyama, Tomo-Hiko Watanabe, Yasuhiro Idomura, Motoki Nakata, Masanori Nunami, and Akihiro Ishizawa, Plasma and Fusion Research 8, 1403150 (2013).
https://doi.org/10.1585/pfr.8.1403150
ジャイロ運動論における並列FFTの高速計算手法を開発した。マルチストリームの並列2次元FFTを行う際に、波数空間のデータ転置に係わるMPI通信時間を隠ぺいするために、独立な座標についてのパイプライン化とOpenMPを用いた通信と演算のオーバーラップを行った。いくつかのオーバーラップ方法について検討し、計算時間の理論見積もりとの一致や、演算性能の向上を示した。
“Numerical techniques for parallel dynamics in electromagnetic gyrokinetic Vlasov simulations”, Shinya Maeyama, Akihiro Ishizawa, Tomo-Hiko Watanabe, Noriyoshi Nakajima, Shunji Tsuji-Iio, and Hiroaki Tsutsui, Computer Physics Communications 184, 2462 (2013).
https://doi.org/10.1016/j.cpc.2013.06.014
Delta-fジャイロ運動論シミュレーションでしばしば現れる磁力線方向の数値振動について調べ、差分化誤差による格子振動の線形成長、バルーニング角の有限性による境界条件、非線形性によるエイリアシング誤差などの性質を明らかにした。フィルターや人工粘性、固定/流出境界条件を用いた場合の比較を行い、エントロピーバランス、線形成長率、乱流輸送フラックス等への影響を議論した。
“A hybrid method of semi-Lagrangian and additive semi-implicit Runge–Kutta schemes for gyrokinetic Vlasov simulations”, Shinya Maeyama, Akihiro Ishizawa, Tomo-Hiko Watanabe, Noriyoshi Nakajima, Shunji Tsuji-Iio, and Hiroaki Tsutsui, Computer Physics Communications 183, 1986 (2012).
https://doi.org/10.1016/j.cpc.2012.04.028
セミラグランジアン法をdelta-fジャイロ運動論に適用することでシミュレーションを高速化できるかという試みその2。作用素分割法を用いて、線形移流に帰着する磁力線平行方向の運動には高精度セミラグランジアン法を、スペクトル展開された磁力線垂直方向の運動には加法的半陰的ルンゲクッタ法を用いることで、線形項によるCFL条件フリーな数値解法を考案し、断熱的電子モデルにおけるイオン温度勾配不安定性の計算に適用した。磁力線方向のCFL条件が厳しくなるステラレータ系のジャイロ運動論シミュレーションを高速化できることを実証した。(しかしながら、この数値スキームをそのまま電磁的ジャイロ運動論方程式に適応した場合は数値不安定性となってしまった。最近になって、研究室の学生らと一緒に解法の再検討を行い、モーメント分離法というアイディアでうまくいきそうな見込み[渡邊裕介他,日本物理学会2016年秋季大会]。)
“A Numerical Method for Parallel Particle Motions in Gyrokinetic Vlasov Simulations”, Shinya Maeyama, Akihiro Ishizawa, Tomo-Hiko Watanabe, Noriyoshi Nakajima, Shunji Tsuji-Iio, and Hiroaki Tsutsui, Plasma and Fusion Research 6, 2401028 (2011).
https://doi.org/10.1585/pfr.6.2401028
セミラグランジアン法をdelta-fジャイロ運動論に適用することでシミュレーションを高速化できるかという試みその1。
"Effects of time-varying ExB flow on slab ion-temperature-gradient turbulence”, Shinya Maeyama, Akihiro Ishizawa, Tomo-Hiko Watanabe, Milos M. Skoric, Noriyoshi Nakajima, Shunji Tsuji-Iio, and Hiroaki Tsutsui, Physics of Plasmas 17, 062305 (2010).
https://doi.org/10.1063/1.3432121
イオン温度勾配不安定性駆動乱流の二流体シミュレーションを行い、帯状流ポテンシャルを人為的に与えた場合に、乱流揺動がどのように応答するかを調べた。この論文の特徴的な点は、時間変化しない定常帯状流と時間振動する帯状流が混在する場合、帯状流による乱流抑制効果を打ち消しあう場合があることが示されたことである。帯状流の振幅・周波数を変えて、乱流の応答特性を議論した。(最初の主著論文であり、修士学生時分の私が半ば押しかけて始まった核融合研との共同研究が結実した成果として思い出深い。)
